Quantative Risk Management 1/4 - Risk and Return

Posted on | Post modified: | In

Datacamp: https://campus.datacamp.com/courses/quantitative-risk-management-in-python

Course Description
Managing risk using Quantitative Risk Management is a vital task across the banking, insurance, and asset management industries. It’s essential that financial risk analysts, regulators, and actuaries can quantitatively balance rewards against their exposure to risk. This course introduces you to financial portfolio risk management through an examination of the 2007—2008 financial crisis and its effect on investment banks such as Goldman Sachs and J.P. Morgan. You’ll learn how to use Python to calculate and mitigate risk exposure using the Value at Risk and Conditional Value at Risk measures, estimate risk with techniques like Monte Carlo simulation, and use cutting-edge technologies such as neural networks to conduct real time portfolio rebalancing.

1/4 Object:

  1. understanding of risk and return
  2. how risk and return are related to each other,
  3. identify risk factors, and use them to re-acquaint ourselves with Modern Portfolio Theory applied to the global financial crisis of 2007-2008.

Introduction

  • Quantitative Risk Management: Study of quantifiable uncertainty
  • Uncertainty: (1) Future outcome (2) Outcomes impact planning decisions
  • Risk Management: mitigate (reduce effects of) adverse outcomes
  • Quantifiable uncertainty: identify fators to measure risk (what factors can cause the uncertainty)
  • This project: Focus upon risk associated with a financial portfolio

This project

The Great Recession (2007-2010)

  • Global growth loss more than $2 trillion
  • United States: nearly $10 trillion lost in household wealth
  • U.S. stock markets lost c. $8 trillion in value

Global Finacial Crisis (2007-2009)

  • Large-scale changes in fundamental asset values
  • Massive uncertainty about future returns
  • High asset returns volatility
  • Risk management critical to success or failure

Financial portpolios

  • Collection of assets with uncertain future returns
  • Stocks
  • Bonds
  • Foreign exchange holdings (‘forex’)
  • Stock options

Challenge: Quantify risk to manage uncertainty

  • Make optimal investment decisions
  • Maximize portfolio return, conditional on risk appetite

Quantifying return

Portfolio return: weighted sum of individual asset returns

  • pandas data analysis library
  • DataFrame prices
  • .pct_change() method
1
2
3
4
prices = pandas.read_csv("portfolio.csv")
returns = prices.pct_change()
weights = (weight_1, weight_2, ...)
portfolio_returns = returns.dot(weights)

Quantifying risk

  • Portfolio return volatility = risk
  • Calculate volatility(波动率) via covariance matrix（协方差矩阵）
  • Use .cov() DataFrame method of returns and anaualize
  • Diagonal of covariance is individual assets variances
  • Off-diagonal of covariance are covariances between assets
Assets 1 Assets 2 Assets 3 Assets 4
Assets 1 Diagonal Off-diagonal Off-diagonal Off-diagonal
Assets 2 Off-diagonal Diagonal Off-diagonal Off-diagonal
Assets 3 Off-diagonal Off-diagonal Diagonal Off-diagonal
Assets 4 Off-diagonal Off-diagonal Off-diagonal Diagonal 
1
2
3
covariance = returns.cov()*252
# 252 is the number of trading days
print(covariance)

Portfolio risk

The portfolio variance is a quadratic function of the weights given the covariance matrix, which can be computed in Python using the “At” operator. The variance is usually then transformed into the standard deviation, resulting in the portfolio’s volatility. Both variance and standard deviation are used as measures of volatility.

  • Depends upon asset weights in portfolio
  • Portfolio variance (方差) = weight矩阵转置 covariance 协方差 weight
  • Matrix multiplication can be computed using @ operator in python
  • Standard deviation (标准差) is usually used instead of variance （方差）, 标准差是方差的平方根
1
2
3
weights = [0.25, 0.25, 0.25, 0.25]
portfolio_variance = np.transpose(weights) @ covariance @ weights
portfolio_volatility = np.sart(protforlio_variance)

Volotility time series（时间序列）

  • Can also calculate portfolio volatility over time
  • Use a ‘window’ to comput volatiity over a fixed time period (e.g. a week, 30-day ‘month’)
  • series.rolling() creates a window
  • Observe volatility trend and possible extreme events
1
2
3
windowed = portfolio_returns.rolling(30)
volotility = windowed.std()*np.sqrt(252)
volatility.plot().set.ylable("Standard Deviation, 20-day window")

Excercises

quantifying the effects of uncertainty on a financial portfolio

examine the portfolio’s return

1
2
3
4
5
6
# Select portfolio asset prices for the middle of the crisis, 2008-2009
asset_prices = portfolio.loc['2008-01-01':'2009-12-31']

# Plot portfolio's asset prices during this time
asset_prices.plot().set_ylabel("Closing Prices, USD")
plt.show()

closing price

1
2
3
4
5
6
7
# Compute the portfolio's daily returns
asset_returns = asset_prices.pct_change()
portfolio_returns = asset_returns.dot(weights)

# Plot portfolio returns
portfolio_returns.plot().set_ylabel("Daily Return, %")
plt.show()

daily returns

assess the riskiness of the portfolio using the covariance matrix to determine the portfolio’s volatility

1
2
3
4
5
6
7
8
9
10
11
12
13
# Generate the covariance matrix from portfolio asset's returns
covariance = asset_returns.cov()

# Annualize the covariance using 252 trading days per year
covariance = covariance * 252

# Display the covariance matrix
print(covariance)
                Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        1.475195        0.821707       0.573790     0.724639
Morgan Stanley  0.821707        1.298341       0.658895     0.560523
Goldman Sachs   0.573790        0.658895       0.500807     0.426979
J.P. Morgan     0.724639        0.560523       0.426979     0.685584

Q: Which portfolio asset has the highest annualized volatility over the time period 2008 - 2009?
A: Citibank
(the highest along the diagonal of the covariance matrix.)

1
2
3
4
5
# Compute and display portfolio volatility for 2008 - 2009
portfolio_variance = np.transpose(weights) @ covariance @ weights
portfolio_volatility = np.sqrt(portfolio_variance)
print(portfolio_volatility)
0.8475328513962702
1
2
3
4
5
6
7
8
9
# Calculate the 30-day rolling window of portfolio returns
returns_windowed = portfolio_returns.rolling(30)

# Compute the annualized volatility series
volatility_series = returns_windowed.std()*np.sqrt(252)

# Plot the portfolio volatility
volatility_series.plot().set_ylabel("Annualized Volatility, 30-day Window")
plt.show()

series volatility

Risk factors and financial crisis

Risk factors

  • Valatility: measure of dispersion(离散程度) of resturns around expected value
  • Time series: expected value = sample average
  • What drives expectation and dispersion?
  • Risk factors: variables or events driving portfolio return and volatility

Risk exposure

Risk exposure: meausre of possible portfolio loss
Risk factors determine risk exposure

Risk Factors

Type of risk definition example
Systematic risk （系统性风险） affect volatility of all portfolio assets e.g. airplane engine failure
Market risk systematic risk from general financial market movements price level changes, i.e. inflation; interest rate changes; Economic climate changes
Idiosyncratic risk （特殊风险，非系统性） risk specific to a particular asset/asset class terbulence and the unfastened seatbelt; Bond portfolio: issuer risk of default（违约风险）; Firm/sector characteristics: Firm size （market captalization, 市值）, Book-to-market(股价净值比) issue, Sector shocks (冲击)

Factor models

Factor model: assessment of risk factors affecting portfolio return
Satistical regression (统计回归)：e.g. Ordinary Least Squares (普通最小二乘法/线性回归)
_ dependent variable （因变量）: return (or volatility)

  • independent variable （自变量）: systemic and/or idosyncratice risk factors
    Fama-French factor model: combination of
  • market risk and
  • idiosycratic risk (firm size, firm value)

Crisis risk factor: mortgage-backed securities （MBS 不动产抵押贷款证券）

Investment banks: borrowed heavily just before the crisis （金融危机前大量发债）
Collateral: mortgage-backed securities
MBS: supposed to siversify risk by holdings

  • Flaw: mortgage default risk in fact was highly correlated （违约风险高度相关）
  • Avalanche of delinquencies （拖延雪崩）/ default destroyed collateral value(抵押价值被破坏)
    90-day mortgage delinquency (90天抵押贷款拖欠): risk factor for investment bank portfolio during the crisis

Factor model regression: portfolio returns vs. mortagage delinquency
Import statsmodels.api library for regression tools
Fit regression using .OLS() object and its .fit() method
Display results using regression’s .summary method

1
2
3
import statsmodels.api as sm
regression = sm.OLS(return, delinquencies).fit()
print(regression.summary())

It is the statistical significance of the regression coefficient (回归系数) for mortgage delinquencies that concerns us most.

Exercises

Frequency resampling primer

Risk factor models often rely upon data that is of different frequencies. A typical example is when using quarterly macroeconomic data, such as prices, unemployment rates, etc., with financial data, which is often daily (or even intra-daily). To use both data sources in the same model, higher frequency data needs to be resampled to match the lower frequency data.

The DataFrame and Series Pandas objects have a built-in .resample() method that specifies the lower frequency. This method is chained with a method to create the lower-frequency statistic, such as .mean() for the average of the data within the new frequency period, or .min() for the minimum of the data.

1
2
3
4
5
6
7
8
9
10
11
12
13
# Convert daily returns data to weekly and quarterly frequency

# 1. Convert daily returns to quarterly average returns
returns_q = returns.resample('Q').mean()

# Examine the beginning of the quarterly series
print(returns_q.head)

# 2. Convert daily returns to weekly minimum returns
returns_w = returns.resample('W').min()

# Examine the beginning of the weekly series
print(returns_w.head)

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
<bound method NDFrame.head of Date
2004-12-31         NaN
2005-03-31   -0.000367
2005-06-30   -0.000366
2005-09-30    0.000615
2005-12-31    0.001323
2006-03-31    0.001384
2006-06-30    0.000084
2006-09-30    0.001654
2006-12-31    0.001717
2007-03-31   -0.000200
2007-06-30    0.000509
2007-09-30   -0.001446
2007-12-31   -0.002300
2008-03-31   -0.002337
2008-06-30   -0.002166
2008-09-30    0.000943
2008-12-31   -0.003480
2009-03-31    0.002415
2009-06-30    0.004946
2009-09-30    0.004516
2009-12-31   -0.001940
2010-03-31    0.001330
2010-06-30   -0.002688
2010-09-30    0.001088
2010-12-31    0.002328
Freq: Q-DEC, dtype: float64>
<bound method NDFrame.head of Date
2005-01-02         NaN
2005-01-09   -0.011152
2005-01-16   -0.007643
2005-01-23   -0.011076
2005-01-30   -0.000443
                ...   
2010-12-05   -0.009894
2010-12-12    0.001379
2010-12-19   -0.016622
2010-12-26   -0.005974
2011-01-02   -0.007729
Freq: W-SUN, Length: 314, dtype: float64>

Visualizing risk factor correlation

Investment banks heavily invested in mortgage-backed securities (MBS) before and during the financial crisis. This makes MBS a likely risk factor for the investment bank portfolio.

Assess this using scatterplots between portfolio_returns and an MBS risk measure, the 90-day mortgage delinquency rate mort_del.

1
2
3
4
5
6
7
8
9
10
11
12
# Transform the daily portfolio_returns into quarterly average returns
portfolio_q_average = portfolio_returns.resample('Q').mean().dropna()

# Create a scatterplot between delinquency and quarterly average returns
plot_average.scatter(mort_del, portfolio_q_average)

# Transform daily portfolio_returns returns into quarterly minimum returns
portfolio_q_min = portfolio_returns.resample('Q').min().dropna()

# Create a scatterplot between delinquency and quarterly minimum returns
plot_min.scatter(mort_del, portfolio_q_min)
plt.show()

visualize correlation

Least-squares factor model

As we can see, there is a negative correlation between minimum quarterly returns and mortgage delinquency rates from 2005 - 2010. This can be made more precise with an OLS regression factor model.

Dependent variables: average returns, minimum returns, and average volatility.
Independent variable: the mortgage delinquency rate.

In the regression summary, examine the coefficients’ t-statistic for statistical significance, as well as the overall R-squared for goodness of fit.

The statsmodels.api library is available as sm.

1
2
3
4
5
6
7
8
# Add a constant to the regression
mort_del = sm.add_constant(mort_del)

# Create the regression factor model and fit it to the data
results = sm.OLS(port_q_mean, mort_del).fit()

# Print a summary of the results
print(results.summary())

分别比较三个因变量的回归系数

  1. results = sm.OLS(port_q_mean, mort_del).fit()
  2. results = sm.OLS(port_q_min, mort_del).fit()
  3. results = sm.OLS(vol_q_mean, mort_del).fit()

results = sm.OLS(port_q_mean, mort_del).fit() 结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.021
Model:                            OLS   Adj. R-squared:                 -0.023
Method:                 Least Squares   F-statistic:                    0.4801
Date:                Sat, 09 Jan 2021   Prob (F-statistic):              0.496
Time:                        05:15:21   Log-Likelihood:                 113.89
No. Observations:                  24   AIC:                            -223.8
Df Residuals:                      22   BIC:                            -221.4
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
=============================================================================================
                                coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------
const                        -0.0001      0.001     -0.175      0.862      -0.002       0.002
Mortgage Delinquency Rate     0.0083      0.012      0.693      0.496      -0.016       0.033
==============================================================================
Omnibus:                        0.081   Durbin-Watson:                   1.604
Prob(Omnibus):                  0.960   Jarque-Bera (JB):                0.293
Skew:                          -0.071   Prob(JB):                        0.864
Kurtosis:                       2.477   Cond. No.                         26.7
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

results = sm.OLS(port_q_min, mort_del).fit()结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.178
Model:                            OLS   Adj. R-squared:                  0.141
Method:                 Least Squares   F-statistic:                     4.761
Date:                Sat, 09 Jan 2021   Prob (F-statistic):             0.0401
Time:                        05:17:56   Log-Likelihood:                 39.937
No. Observations:                  24   AIC:                            -75.87
Df Residuals:                      22   BIC:                            -73.52
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
=============================================================================================
                                coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------
const                        -0.0279      0.017     -1.611      0.121      -0.064       0.008
Mortgage Delinquency Rate    -0.5664      0.260     -2.182      0.040      -1.105      -0.028
==============================================================================
Omnibus:                       13.525   Durbin-Watson:                   0.513
Prob(Omnibus):                  0.001   Jarque-Bera (JB):               12.333
Skew:                          -1.534   Prob(JB):                      0.00210
Kurtosis:                       4.710   Cond. No.                         26.7
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

results = sm.OLS(vol_q_mean, mort_del).fit()结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.190
Model:                            OLS   Adj. R-squared:                  0.154
Method:                 Least Squares   F-statistic:                     5.174
Date:                Sat, 09 Jan 2021   Prob (F-statistic):             0.0330
Time:                        05:22:24   Log-Likelihood:                 60.015
No. Observations:                  24   AIC:                            -116.0
Df Residuals:                      22   BIC:                            -113.7
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
=============================================================================================
                                coef    std err          t      P>|t|      [0.025      0.975]
---------------------------------------------------------------------------------------------
const                         0.0100      0.007      1.339      0.194      -0.006       0.026
Mortgage Delinquency Rate     0.2558      0.112      2.275      0.033       0.023       0.489
==============================================================================
Omnibus:                       19.324   Durbin-Watson:                   0.517
Prob(Omnibus):                  0.000   Jarque-Bera (JB):               23.053
Skew:                           1.814   Prob(JB):                     9.87e-06
Kurtosis:                       6.145   Cond. No.                         26.7
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Morden portforlio throry

The risk-return trade-off

Risk factors: sources of uncertainty affecting return
Intuitively(直觉): greater undcertainty (more risk) compensated by greater return
Cannot guarantee return: need some meaure of expected return

  • average (mean) historical return: proxy for expected future return

Investor risk appetite

Investor survey: minimum return required for given level of risk?
Survey response creates (risk. return) risk profile “data point”
Vary risk level => set of (risk, return) points
Investor risk appetite (风险偏好): defines one quantified relationship between risk and return

Choosing portfolio weights

Vary portforlio weights of given portforlio => creates set of (risk, return) pairs
Changing weights = beginning of risk management!
Goal: change weights to maximize expected return, given risk level

  • Eyuivalently: minimize risk, given expected return level
    Changing weights = adjusting investors’ risk exposure

Morden portforlio throry (MPT)

Efficient portfolio: portfolio with weights generating highest expected return pf given level of risk

The efficient frontier （有效前沿/效率前沿模型）

  • Compute many efficient portfolios for different levels of risk
  • Efficient frontier（有效边界）: locus (轨迹) of (risk, return) pairs created by efficient portfolios
  • 有效边界是在收益—风险约束条件下能够以最小的风险取得最大的收益的各种证券的集合
  • 处于有效边界上的组合称为有效组合（Efficient Portfolio）

PyPortfolioOpt library: optimized tools for MPT
EfficientFrontier class: generates one optimal portfolio at a time
Constrained Line Algorithm (边界算法) class: generate the entire efficient frontier

  • Requires covariance matrix of returns)
  • Requires proxy for expected future returns: mean historical returns

Invesrment bank portfolio 2005-2010

Expected returns: historical data
Covariance matrix: Covariance Shrinkage improved efficiency of estimate
Constrained Line Algorithm object CLA
Minimum variance portfolio: cla.min_volatility()
Efficient frontier: cla.efficient_frontier()

1
2
3
4
5
expected returns = mean_historical_return(prices)
efficient_cov = CovarianceShrinkage(prices).ledoit_wolf()
cla = CLA(expected_returns, efficient_cov)
minimum_variance = cla,min_volatility()
(ret, vol. weights) = cla.efficient_frontier()

Visualizing the efficient frontier

scatter plot of (vol, ret) pairs
Minimum variance portfolio （最小方差投资组合）: smallest volatility of all possible efficient portfolios
Increase risk appetite (增加风险承受能力): move along the frontier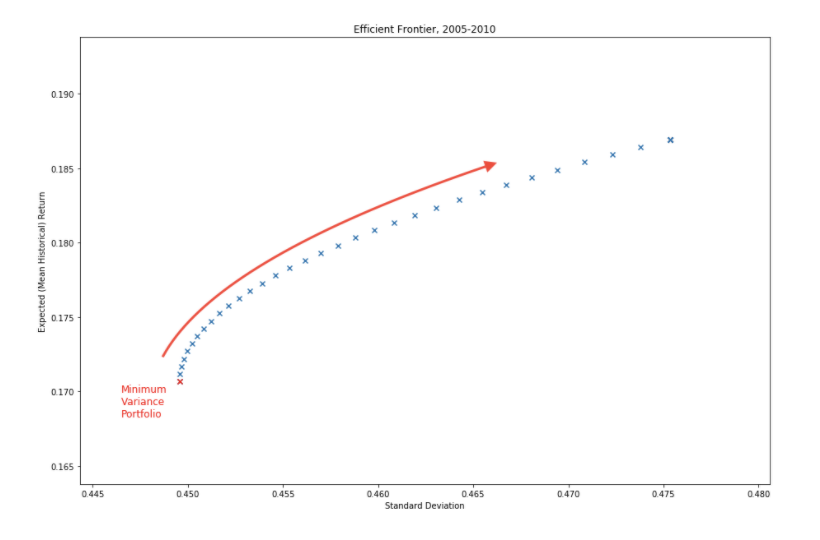
Efficient frontier

Excercises

Practice with PyPortfolioOpt: returns

Modern Portfolio Theory is the cornerstone of portfolio risk management, because the efficient frontier is a standard method of assessing both investor risk appetite and market risk-return tradeoffs. In this exercise you’ll develop powerful tools to explore a portfolio’s efficient frontier, using the PyPortfolioOpt pypfopt Python library.

To compute the efficient frontier, both expected returns and the covariance matrix of the portfolio are required.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Load the investment portfolio price data into the price variable.
prices = pd.read_csv("portfolio.csv")

# Convert the 'Date' column to a datetime index
prices['Date'] = pd.to_datetime(prices['Date'], format='%d/%m/%Y')
prices.set_index(['Date'], inplace = True)

# Import the mean_historical_return method
from pypfopt.expected_returns import mean_historical_return

# Compute the annualized average historical return
mean_returns = mean_historical_return(prices, frequency = 252)

# Plot the annualized average historical return
plt.plot(mean_returns, linestyle = 'None', marker = 'o')
plt.show()

PyPortfolioOpt_return

Practice with PyPortfolioOpt: covariance

Portfolio optimization relies upon an unbiased and efficient estimate of asset covariance. Although sample covariance is unbiased, it is not efficient—extreme events tend to be overweighted.

One approach to alleviate this is through “covariance shrinkage”, where large errors are reduced (‘shrunk’) to improve efficiency. In this exercise, you’ll use pypfopt.risk_models‘s CovarianceShrinkage object to transform sample covariance into an efficient estimate. The textbook error shrinkage method, .ledoit_wolf(), is a method of this object.

Asset prices are available in your workspace. Note that although the CovarianceShrinkage object takes prices as input, it actually calculates the covariance matrix of asset returns, not prices.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Import the CovarianceShrinkage object
from pypfopt.risk_models import CovarianceShrinkage

# Create the CovarianceShrinkage instance variable
cs = CovarianceShrinkage(prices)

# Compute the sample covariance matrix of returns
sample_cov = prices.pct_change().cov() * 252

# Compute the efficient covariance matrix of returns
e_cov = cs.ledoit_wolf()

# Display both the sample covariance_matrix and the efficient e_cov estimate
print("Sample Covariance Matrix\n", sample_cov, "\n")
print("Efficient Covariance Matrix\n",e_cov, "\n")

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
Sample Covariance Matrix
                 Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        0.536214        0.305045       0.217993     0.269784
Morgan Stanley  0.305045        0.491993       0.258625     0.218310
Goldman Sachs   0.217993        0.258625       0.217686     0.170937
J.P. Morgan     0.269784        0.218310       0.170937     0.264315 

Efficient Covariance Matrix
                 Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        0.527505        0.288782       0.206371     0.255401
Morgan Stanley  0.288782        0.485642       0.244837     0.206671
Goldman Sachs   0.206371        0.244837       0.225959     0.161823
J.P. Morgan     0.255401        0.206671       0.161823     0.270102

Breaking down the financial crisis

n the video you saw the efficient frontier for the portfolio of investment banks over the entire period 2005 - 2010, which includes time before, during and after the global financial crisis.

Here you’ll break down this period into three sub-periods, or epochs: 2005-2006 (before), 2007-2008 (during) and 2009-2010 (after). For each period you’ll compute the efficient covariance matrix, and compare them to each other.

The portfolio’s prices for 2005 - 2010 are available in your workspace, as is the CovarianceShrinkage object from PyPortfolioOpt.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Create a dictionary of time periods (or 'epochs')
epochs = { 'before' : {'start': '1-1-2005', 'end': '31-12-2006'},
           'during' : {'start': '1-1-2007', 'end': '31-12-2008'},
           'after'  : {'start': '1-1-2009', 'end': '31-12-2010'}
         }

# Compute the efficient covariance for each epoch
e_cov = {}
for x in epochs.keys():
  sub_price = prices.loc[epochs[x]['start']:epochs[x]['end']]
  e_cov[x] = CovarianceShrinkage(sub_price).ledoit_wolf()

# Display the efficient covariance matrices for all epochs
print("Efficient Covariance Matrices\n", e_cov)

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Efficient Covariance Matrices
 {'before':                 Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        0.018149        0.013789       0.013183     0.013523
Morgan Stanley  0.013789        0.043021       0.030559     0.016525
Goldman Sachs   0.013183        0.030559       0.044482     0.018237
J.P. Morgan     0.013523        0.016525       0.018237     0.024182, 'during':                 Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        0.713035        0.465336       0.323977     0.364848
Morgan Stanley  0.465336        0.994390       0.434874     0.298613
Goldman Sachs   0.323977        0.434874       0.408773     0.224668
J.P. Morgan     0.364848        0.298613       0.224668     0.422516, 'after':                 Citibank  Morgan Stanley  Goldman Sachs  J.P. Morgan
Citibank        0.841156        0.344939       0.252684     0.356788
Morgan Stanley  0.344939        0.388839       0.231624     0.279727
Goldman Sachs   0.252684        0.231624       0.244539     0.223740
J.P. Morgan     0.356788        0.279727       0.223740     0.382494}

The efficient frontier and the financial crisis

Previously we examined the covariance matrix of the investment bank portfolio before, during and after the financial crisis. Now we will visualize the changes that took place in the efficient frontier, showing how the crisis created a much higher baseline risk for any given return.

Using the PyPortfolioOpt pypfopt library’s Critical Line Algorithm (CLA) object, we can derive and visualize the efficient frontier during the crisis period, and add it to a scatterplot already displaying the efficient frontiers before and after the crisis.

Expected returns returns_during and the efficient covariance matrix ecov_during are available, as is the CLA object from pypfopt. (Remember that DataCamp plots can be expanded to their own window, which can increase readability.)

1
2
3
4
5
6
7
8
9
10
11
12
13
# Initialize the Crtical Line Algorithm object
efficient_portfolio_during = CLA(returns_during, ecov_during)

# Find the minimum volatility portfolio weights and display them
print(efficient_portfolio_during.min_volatility())

# Compute the efficient frontier
(ret, vol, weights) = efficient_portfolio_during.efficient_frontier()

# Add the frontier to the plot showing the 'before' and 'after' frontiers
plt.scatter(vol, ret, s = 4, c = 'g', marker = '.', label = 'During')
plt.legend()
plt.show()

The efficient frontier