Quantative Risk Management 2/4 - Goal-oriented risk management

Posted on | Post modified: | In

2/4 Object:

  1. expand your portfolio optimization toolkit with risk measures such as Value at Risk (VaR) and Conditional Value at Risk (CVaR)
  2. use specialized Python libraries including pandas, scipy, and pypfopt.
  3. how to mitigate risk exposure using the Black-Scholes model to hedge an options portfolio.

Measuring Risk

The Loss Distribution

Forex example:
EUR and USD (exchange rate is r)
r EUR = 1 USD
Loss = EUR 100 x (1-r)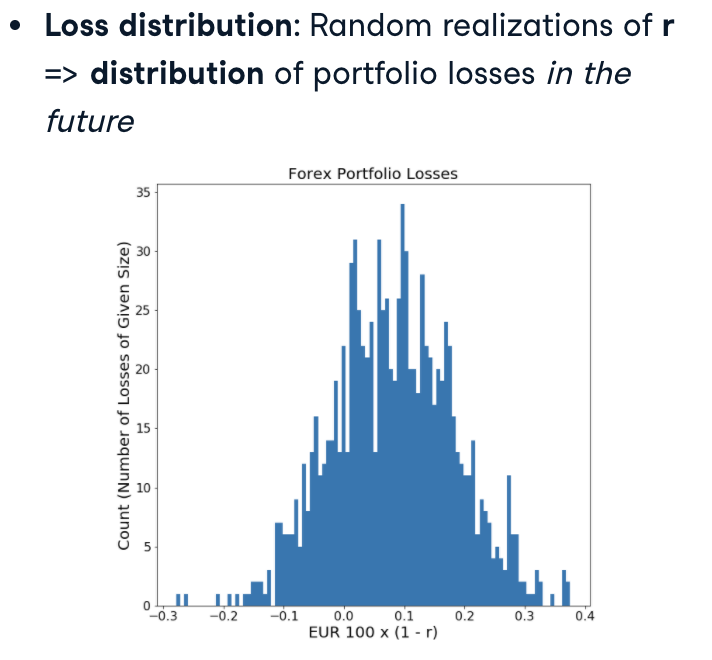
Loss Distribution

random realization of r => distribution of portfolio losses in the future

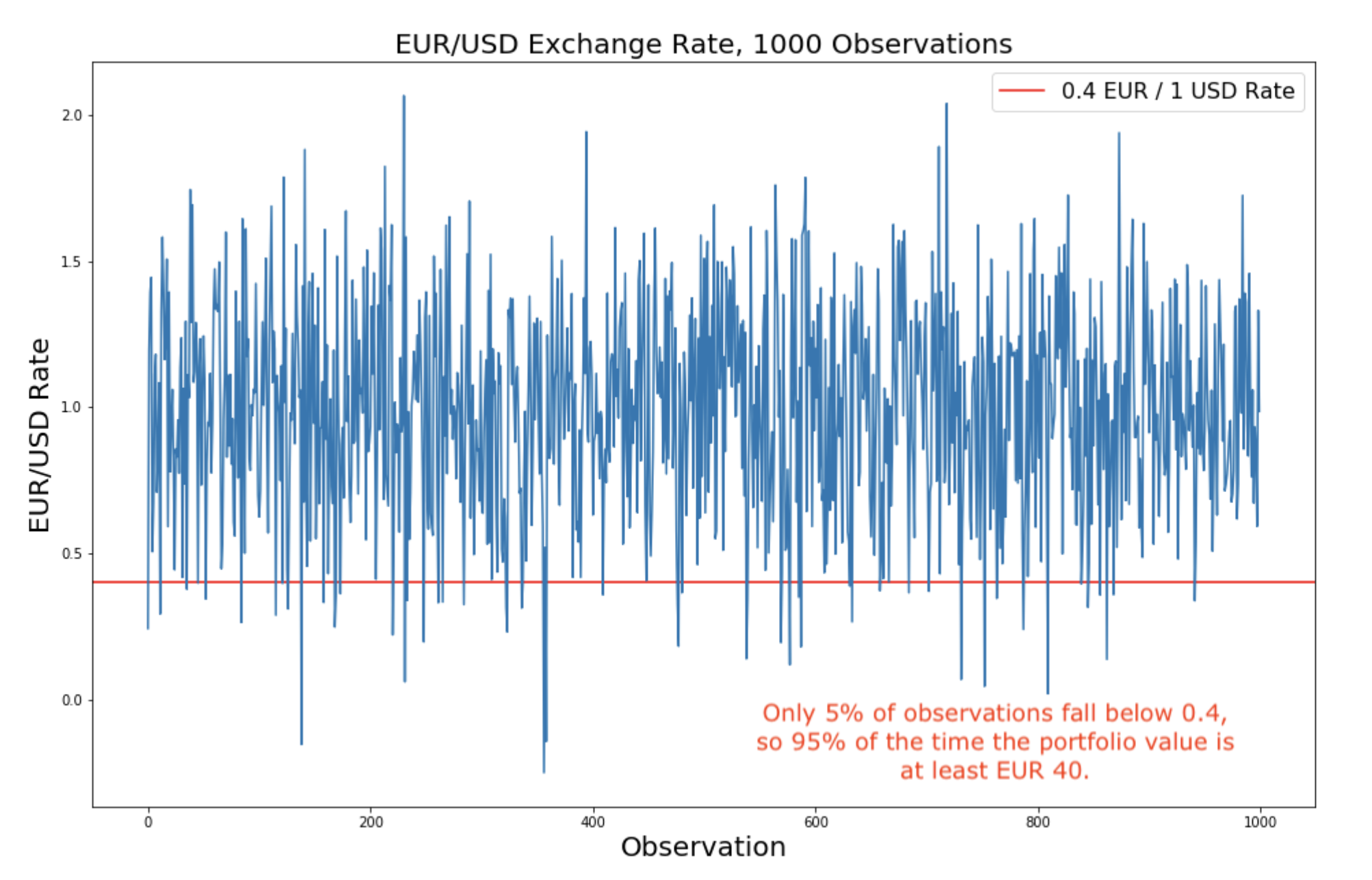
Maximum loss

What’s the max loss of a portforlio?
Losses cannot be bounded with 100% certainty
Confidence level: replace 100% certainty with likelyhood of upper bound
Can express questions like “what’s the maximum loss that would take place 95% of the time?”

  • here the confidence level is 95%

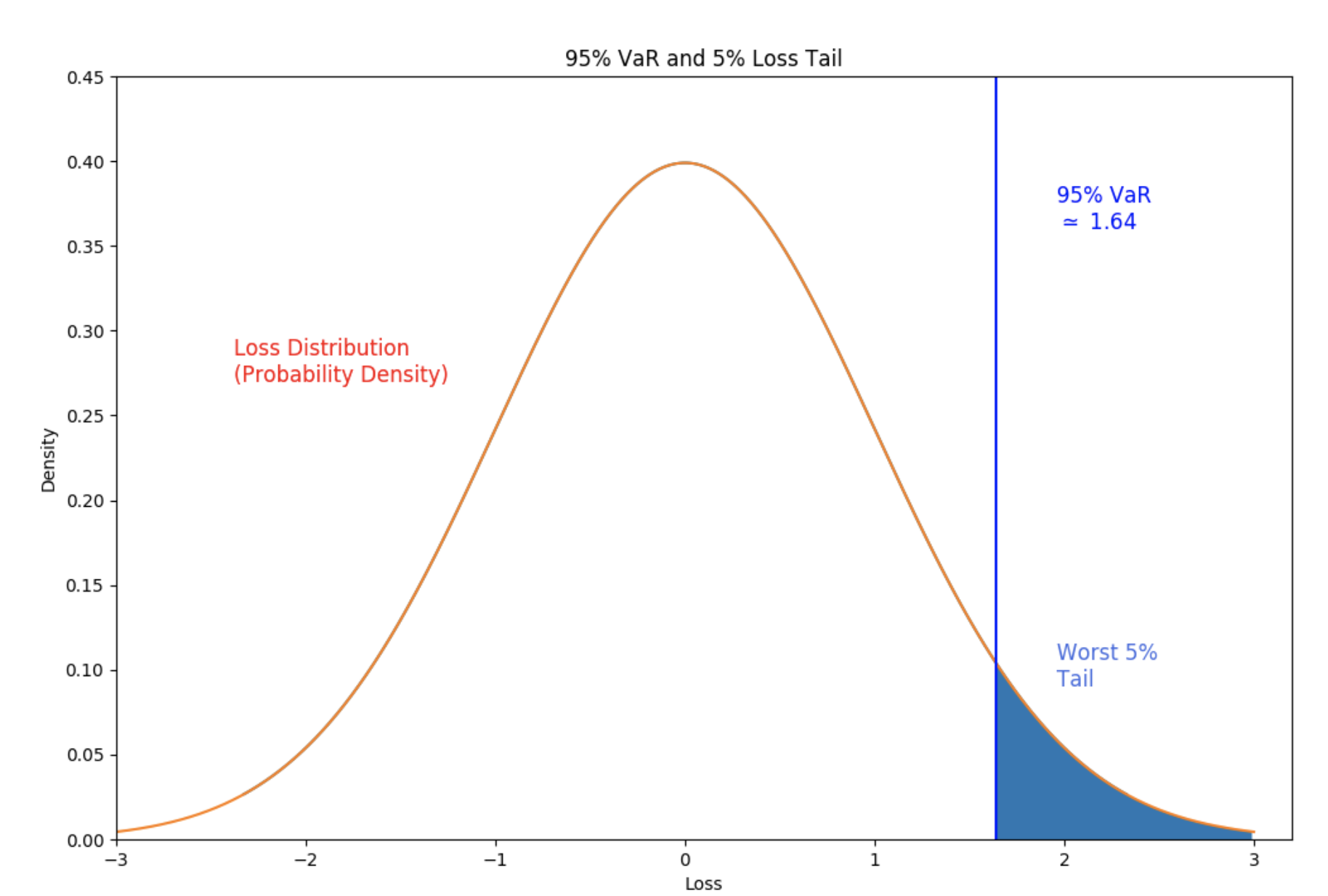
Value at risk (VaR)

VaR（风险价值）: statistic measuring maximum portfolio loss at a particular confidence level

某一置信度下的最大损失

Typical confidence levels: 95%, 99%, and 99.5% (usually represented as decimals)

VaR
Forex example:

Conditional Value at Risk (CVaR)

CVaR（条件风险价值）: measures expected loss given a minimum loss equal to the VaR. It equals expected value of the tail of the loss distribution

VaR的一个问题是他不考虑超过该置信度后的损失情况, 而CVaR表示投资组合的损失超过某个给定VaR值的条件下，该投资组合的平均损失值。

CVaR

Deriving the VaR

  1. Specify the confidence level (e.g. 95%, 0.95)
  2. Creat a Series of loss observations
  3. Compute loss.quantile() at specified confidence level
  4. VaR = computed .quantile() at desired confidence level
1
2
3
loss = pd.Series(observations)
VaR = loss.quantile(0.95)
print ("VaR_95= ", VaR_95)

If we know losses are distributed according to a statistical distribution like the Normal distribution, we can also use the “.ppf()”, or percent point function, to find the VaR.

—> scipy.stats loss distribution: percent point function .ppf() can also be used.

Deriving the CVaR

  1. Specify the confidence level (e.g. 95%, 0.95)
  2. Creat or use sample from loss distribution
  3. Compute VaR at a specified confidence level
  4. Compute CVaR as expected loss (Normal distribution: scipy.stats.norm.expected() does this)
1
2
3
4
losses = pd.Series(scipy.stats.norm.rvs(size = 1000)
VaR = scipy.stats.norm.ppf(0,95)
CVaR = (1/(1-0.95))*scipy.stats.norm.expect(lambda x: x, lb = VaR_95)
print ("CVaR= ", CVaR)

Visulizing the VaR

Visulizing the VaR
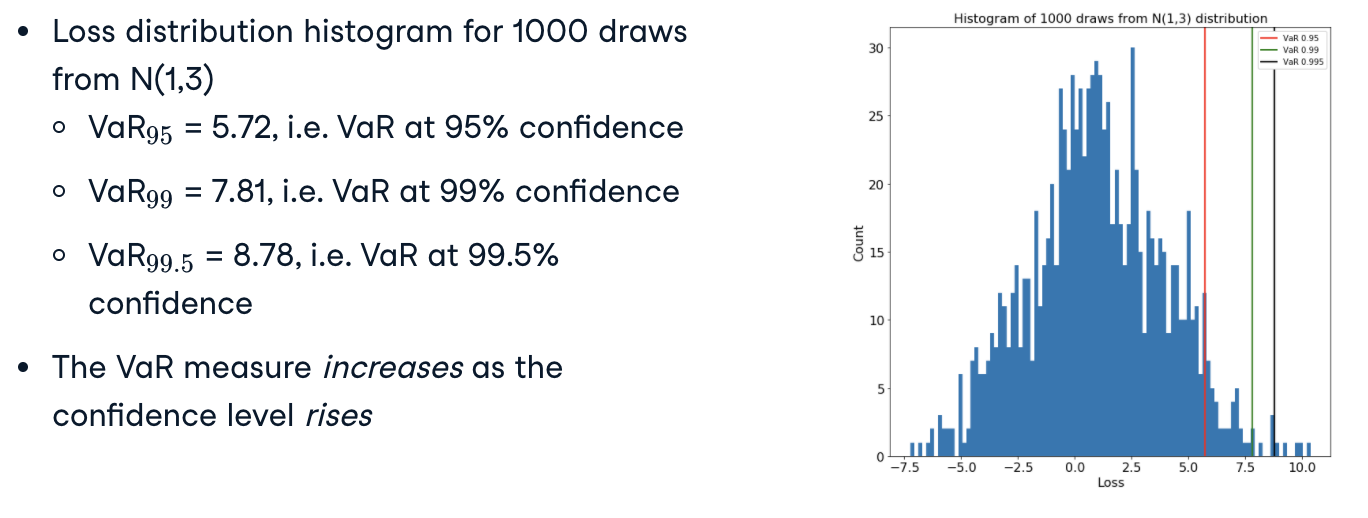
*N(mean, variance) stands for normal distribution

Excercises

VaR for the Normal distribution

To get accustomed to the Value at Risk (VaR) measure, it helps to apply it to a known distribution. The Normal (or Gaussian) distribution is especially appealing as it 1) has an analytically simple form, and 2) represents a wide variety of empirical phenomena. For this exercise you’ll assume that the loss of a portfolio is normally distributed, i.e., the higher the value drawn from the distribution, the higher the loss.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Create the VaR measure at the 95% confidence level using norm.ppf()
VaR_95 = norm.ppf(0.95)

# Create the VaR meaasure at the 5% significance level using numpy.quantile()
draws = norm.rvs(size = 100000)
VaR_99 = np.quantile(draws, 0.99)

# Compare the 95% and 99% VaR
print("95% VaR: ", VaR_95, "; 99% VaR: ", VaR_99)

# Plot the normal distribution histogram and 95% VaR measure
plt.hist(draws, bins = 100)
plt.axvline(x = VaR_95, c='r', label = "VaR at 95% Confidence Level")
plt.legend(); plt.show()

VaR for the Normal Dirstribution

Comparing CVaR and VaR

The conditional value at risk (CVaR), or expected shortfall (ES), asks what the average loss will be, conditional upon losses exceeding some threshold at a certain confidence level. It uses VaR as a point of departure, but contains more information because it takes into consideration the tail of the loss distribution.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Compute the mean and variance of the portfolio returns
pm = portfolio_losses.mean()
ps = portfolio_losses.std()

# Compute the 95% VaR using the .ppf()
VaR_95 = norm.ppf(0.95, loc = pm, scale = ps)
# Compute the expected tail loss and the CVaR in the worst 5% of cases
tail_loss = norm.expect(lambda x: x, loc = pm, scale = ps, lb = VaR_95)
CVaR_95 = (1 / (1 - 0.95)) * tail_loss

# Plot the normal distribution histogram and add lines for the VaR and CVaR
plt.hist(norm.rvs(size = 100000, loc = pm, scale = ps), bins = 100)
plt.axvline(x = VaR_95, c='r', label = "VaR, 95% confidence level")
plt.axvline(x = CVaR_95, c='g', label = "CVaR, worst 5% of outcomes")
plt.legend(); plt.show()

Comparing CVaR and VaR

Risk exposure and loss

Deciding between options

  1. Chances of negaticve shock: probability of loss
  2. Loss associated with shock: amount or conditional amount (e.g. VaR, CVaR)
  3. Desire to avoid shock: Risk tolerance

Risk exposure and VaR

Risk exposure = probability of loss x loss measure
Loss measure: e.g. VaR

loss distribution:
normal distribution: good for large number of samples
students’ t distribution: good for small number of samples

Risk appetite

  • Insurance is a way to pay a fixed value to avoid an uncertain outcome, which is risk-averse behavior.

risk averse (or risk avoiding) - if they would accept a certain payment (certainty equivalent) of less than $50 (for example, $40), rather than taking the gamble and possibly receiving nothing.
risk neutral – if they are indifferent between the bet and a certain $50 payment.

degrees of freedom (df)

number of independent observations

  • Small df: “fat tailed” T distribution
  • Large df: Normal distribution

Exercises

VaR and risk exposure

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Import the Student's t-distribution
from scipy.stats import t

# Create rolling window parameter list
mu = losses.rolling(30).mean()
sigma = losses.rolling(30).std()
rolling_parameters = [(29, mu[i], s) for i,s in enumerate(sigma)]

# Compute the 99% VaR array using the rolling window parameters
VaR_99 = np.array( [ t.ppf(0.99, *params) 
                    for params in rolling_parameters ] )

# Plot the minimum risk exposure over the 2005-2010 time period
plt.plot(losses.index, 0.01 * VaR_99 * 100000)
plt.show()

VaR and risk exposure

CVaR and risk exposure

1
2
3
4
5
6
7
8
9
10
# Fit the Student's t distribution to crisis losses
p = t.fit(crisis_losses)

# Compute the VaR_99 for the fitted distribution
VaR_99 = t.ppf(0.99, *p)

# Use the fitted parameters and VaR_99 to compute CVaR_99
tail_loss = t.expect(lambda y: y, args = (p[0],), loc = p[1], scale = p[2], lb = VaR_99 )
CVaR_99 = (1 / (1 - 0.99)) * tail_loss
print(CVaR_99)

结果为0.3380538488604617

Risk management with VaR and CVaR

Incorporating VaR into MPT

Mordern Portfolio Theory (MPT): “mean-variance” optimization

  • Highest expected return
  • Risk level (volatility) is given
  • Objective function: expected return

VaR/CVaR: measure risk over distribution of loss

Adapt MPT to optimize over loss distribution vs. expected return

A new objective: minimize CVaR

change objective of portfolio optimization

  • mean-variance objective: maximize expected mean return
  • CVaR objective: minimize expected conditional loss at a given confidence level
    —> Optimization: portfolio weights minimizing CVaR
    —> find the lowest expected loss in worst (1-confidence) of possible outcomes
    在给定的置信度下，可能出现的结果中，达到最低的损失

CVaR minimization using PyPortfolioOpt

  1. Create an EfficientFrontier object with an efficient covariance matrix e_cov
  2. Import built-in objective function that minimizes CVaR, negative_cvar() from pypopt.objective_functions module
  3. Comput optimal portfolio weights using .custom_objective() method
    (Arguements of .negative_cvar() added to .custom_objective).
1
2
3
ef = pypopt.objective_frontier.EfficientFrontier(None, e_cov)
from pypopt.objective_functions import negative_cvar
optimal_weights = ef.custom_objective(negative_cvar, returns)

Negative CVaR?

Seek minimum CVaR portfolio at given significance level 1-alpha
Same as finding portfolio that maximizes returns in worst 1-alpha cases

Question: expect objective function to return positive number, or negative?

Optimization can be either:

  • maximize someting or
  • minimize the negative of someting

PyPortfolioOpt solver: minimizes by default

  • so objective function needs to be negative of CVaR returns
  • Give same answer as minimizing CVaR losses

Term “negative CVaR” is a misnormer: CVaR is an expected loss

Mean-variance vs. CVaR risk management

Mean-variance risk management: minimize volatility

  • We compute the minimum volatility portfolio weights in the usual fashion, by creating an EfficientFrontier instance and using the ‘min volatility’ method.
    CVaR risk management: minimize negative CVaR
  • The CVaR-minimizing portfolio is created using the ‘custom objective’ and ‘negative cvar’ methods. The result is a roughly equally-weighted portfolio.
  • This creates more volatility than the minimum volatility mean-variance portfolio, but with the benefit that the worst 5% cases of loss are minimized.

Excercies

VaR from a fitted distribution

Minimizing CVaR requires calculating the VaR at a confidence level, say 95%. Previously you derived the VaR as a quantile from a Normal (or Gaussian) distribution, but minimizing the CVaR more generally requires computing the quantile from a distribution that best fits the data.

1
2
3
4
5
6
7
8
9
10
11
# Visualize the fitted distribution with a plot
x = np.linspace(-0.25,0.25,1000)
plt.plot(x,fitted.evaluate(x))
plt.show()

# Create a random sample of 100,000 observations from the fitted distribution
sample = fitted.resample(100000)

# Compute and display the 95% VaR from the random sample
VaR_95 = np.quantile(sample, 0.95)
print(VaR_95)

VaR from a fitted distribution

Minimizing CVaR

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Import the EfficientFrontier class
from pypfopt.efficient_frontier import EfficientFrontier

# Import the negative_cvar objective function
from pypfopt.objective_functions import negative_cvar

# Create the efficient frontier instance
ef = EfficientFrontier(None, e_cov)

# Find the cVar-minimizing portfolio weights at the default 95% confidence level
optimal_weights = ef.custom_objective(negative_cvar, returns)

# Display the optimal weights
print(optimal_weights)

结果

1
{'Citibank': 0.24991481239515553, 'Morgan Stanley': 0.2497894497565988, 'Goldman Sachs': 0.25013519444333526, 'J.P. Morgan': 0.2501605434049105}

CVaR risk management and the crisis

Derive the 95% CVaR-minimizing portfolio for 2005-2006, 2007-2008, and 2009-2010.

1
2
3
4
5
6
7
8
9
10
# Initialize the dictionary of optimal weights
optimal_weights_dict = {}

# Find and display the CVaR-minimizing portfolio weights at the default 95% confidence level
for x in ['before', 'during', 'after']:
    optimal_weights_dict[x] = ef_dict[x].custom_objective(negative_cvar, returns_dict[x])

# Compare the CVaR-minimizing weights to the minimum volatility weights for the 'before' epoch
print("CVaR:\n", pd.DataFrame.from_dict(optimal_weights_dict['before']), "\n")
print("Min Vol:\n", pd.DataFrame.from_dict(min_vol_dict['before']), "\n")

结果

1
2
3
4
5
6
7
8
9
10
11
12
13
CVaR:
                   Weight
Citibank        0.248754
Morgan Stanley  0.249111
Goldman Sachs   0.250973
J.P. Morgan     0.251162 

Min Vol:
                   Weight
Citibank        0.655621
Morgan Stanley  0.059033
Goldman Sachs   0.029725
J.P. Morgan     0.255621

Portfolio hedging: offsetting risk

Portfolio statbility

VaR/CVaR: potential portfolio loss for given confidence level
Portfolio optimization: “best” portfolio weights

  • But volatility is still presents!
    Institutional investors: stability of portforlio against volatile changes
  • pension funds: c. USD 20 trillion

Example: raning days and sunny days

Investors portfolio: sunglasses company

  • Risk factor: weather (rain)
  • More rain -> lower company value
  • Lower campany value -> lower stock price
  • lower stock price -> lower portfolio value

Second opportunity: umbrella company

  • more rain -> more value

Portfolio: sunglasses & unbrella, more stable —> risk reduced

—-> Hedging: offset volatility with another asset

Hudging instrumentes: options （期权）

derivative hedging strategies (衍生对冲策略)

Hedging is often performed using derivatives to offset a risky asset position.

One of the most basic derivatives is the European option.

  • A European ‘call’ option gives the holder the right (but not the obligation) to _purchase_ a stock for a fixed price X at a particular time M.
  • A European ‘put’ option gives the holder the right (but not the obligation) to _sell_ a stock for a fixed price X at a particular time M.

The stock is called the ‘underlying’ of the option. The market price of the underlying is called the ‘spot’ price ‘S’. The fixed price is called the ’strike’ price ‘X’ and the time ‘M’ is the ‘maturity’.

Exercises

Black-Scholes options pricing

Black-Scholes 期权定价模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Compute the volatility as the annualized standard deviation of IBM returns
sigma = np.sqrt(252) * IBM_returns.std() 

# Compute the Black-Scholes option price for this volatility
value_s = black_scholes(S = 90, X = 80, T = 0.5, r = 0.02, 
                        sigma = sigma, option_type = "call")

# Compute the Black-Scholes option price for twice the volatility
value_2s = black_scholes(S = 90, X = 80, T = 0.5, r = 0.02, 
                sigma = 2*sigma, option_type = "call")

# Display and compare both values
print("Option value for sigma: ", value_s, "\n",
      "Option value for 2 * sigma: ", value_2s)

结果

1
2
Option value for sigma:  12.129167513536352 
Option value for 2 * sigma:  16.24149623118327

Options pricing and the underlying asset

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Select the first 100 observations of IBM data
IBM_spot = IBM[:100]

# Initialize the European put option values array
option_values = np.zeros(IBM_spot.size)

# Iterate through IBM's spot price and compute the option values
for i,S in enumerate(IBM_spot.values):
    option_values[i] = black_scholes(S = S, X = 140, T = 0.5, r = 0.02, 
                        sigma = sigma, option_type = "put")

# Display the option values array
option_axis.plot(option_values, color = "red", label = "Put Option")
option_axis.legend(loc = "upper left")
plt.show()

Options pricing and the underlying asset

Using options for hedging

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# Compute the annualized standard deviation of `IBM` returns
sigma = np.sqrt(252) * IBM_returns.std()

# Compute the Black-Scholes value at IBM spot price 70
value = black_scholes(S = 70, X = 80, T = 0.5, r = 0.02, 
                      sigma = sigma, option_type = "put")
# Find the delta of the option at IBM spot price 70
delta = bs_delta(S = 70, X = 80, T = 0.5, r = 0.02, 
                 sigma = sigma, option_type = "put")

# Find the option value change when the price of IBM falls to 69.5
value_change = black_scholes(S = 69.5, X = 80, T = 0.5, r = 0.02, 
                             sigma = sigma, option_type = "put") - value

print( (69.5 - 70) + (1/delta) * value_change )

结果为0.00459428051019628